유성이의 공부일지(2) - 혼자공부하는 컴퓨터 구조 + 운영체제 2장
02 - 1. 0과 1로 숫자를 표현하는 방법
정보단위
- 컴퓨터는 0 또는 1밖에 이해하지 못함
- 0과 1을 나타내는 가장 작은 정보 단위를 비트라고 함
- 예를 들어 전구 한개로 꺼짐 또는 켜짐 두 가지 상태를 표현할 수 있듯이, 1비트는 0 또는 1, 두가지 정보를 표현 가능
- 프로그램 크기를 말하는 단위에는 바이트, 킬로바이트, 메가바이트, 기가바이트, 테라바이트 등이 있음
- CPU가 한 번에 처리할 수 있는 데이터 크기를 워드라고 함
- 이렇게 정의된 워드의 절반 크기를 하프 워드, 1배 크기를 풀 워드, 2배 크기를 더블 워드라고 함
바이트(byte)
- 여덟 개의 비트를 묶은 단위
- 비트 보다 한 단계 더 큰 단위
- 1바이트 = 8비트, 2의8승 (256)개의 정보 표현 가능
킬로바이트(kilobyte)
- 1바이트 1000개를 묶은 단위
메가바이트(megabyte)
- 1킬로바이트 1000개를 묶은 단위
기가바이트(gigabyte)
- 1메가바이트 1000개를 묶은 단위
테라바이트(terabyte)
- 1기가바이트 1000개를 묶은 단위
이진법
- 수학에서 0과 1만으로 모든 숫자를 표현하는 방법을 이진법이라고 함
- 이진법을 이용하면 1보다 큰 수도 0과 1만으로 표현 가능
- 숫자가 9를 넘어가는 시점에 자리 올림을 하여 0부터 9까지, 열개의 숫자만으로 모든 수를 사용하는 방법을 십진법이라고 함
- 이진법으로 표현한 후를 이진수, 십진법으로 표현한 수를 십진수라고 함

추가로!!
- 예를 들어 숫자 10만 보고 이게 십진수인지 이진수인지 구분하기가 어려움
- 숫자 10를 십진수로 읽으면 10이지만, 이진수로 읽으면 2임
- 이처럼 숫자만으로는 이 수가 어떤 진법으로 표현된 수인지 알 수 없음
- 이런 혼동을 예방하기 위해 이진수 끝에 아래첨자(2)를 붙이거나 이진수 앞에 0b를 붙임
이진수의 음수 표현
- 십진수 음수를 표현하기 위해서는 단순히 숫자 앞에 마이너스 부호를 붙이면 됨
- 하지만 이진수에는 마이너스를 붙이면 컴퓨터에서는 인식 못함x
- 그렇기에 마이너스 부호를 사용하지 않고 0과 1만으로 음수를 표현해야 함
- 0과 1만으로 음수를 표현하는 방법 중 가장 널리 사용되는 방법은 2의 보수를 구해 이 값을 음수로 간주하는 방법임
- 2의 보수의 사전적 의미는 어떤 수를 그보다 큰 2n에서 뺀 값을 의미함
- 예를 들어 11(2)의 2의 보수는 11(2)보다 큰 2n, 즉 100(2) - 11(2) = 01(2)의 값이 나옴
- 2의 보수를 쉽게 설명하자면 모든 0과 1을 뒤집고, 거기에 1을 더한 값으로 이해하면 됨
- 컴퓨터 내부에서 어떤 수를 다룰 때 양수인지 음수인지를 구분하기 위해 플래그를 사용함
십육진법
- 수가 15를 넘어가는 시점에 자리올림을 하는 숫자 표현방식
- 십진수 10,11,12,13,14,15를 십육진수로는 A,B,C,D,E,F로 표기함
- 십육진수도 이진수와 마찬가지로 숫자 뒤에 아래첨자(16)을 붙이거나, 숫자 앞에 0x를 붙여 구분함
- 15(16) - 수학적 표기 방식, 0x15 - 코드상 표기 방식
십육진수를 이진수로 변환하기
ex) 1A2B(16) = 1A2B(2)
1 = 0001
A = 1010
2 = 0010
B = 1011
즉 0001 1010 0010 1011(2)이 1A2B를 이진수로 표현한 값
이진수를 십육진수로 변환하기
ex) 11010101(2)
1101(2)
0101(2)
D(2)
5(2)
즉 11010101(2) = D5(16)
02 - 1. 0과 1로 문자를 표현하는 방법
문자 집합과 인코딩
- 컴퓨터가 인식하고 표현할 수 있는 문자의 모음을 문자 집합이라고 함
- 컴퓨터는 문자 집합에 속해 있는 문자를 이해할 수 있고, 반대로 문자 집합에 속해 있지 않는 문자는 이해 x
- 예를 들어 문자 집합이 {a,b,c,d,e}인 경우, 5개의 문자만 이해 가능
- 문자를 0과 1로 변환해서 컴퓨터가 이해할 수 있도록 하는 과정을 문자 인코딩이라고 함
- 0과 1로 이루어진 문자 코드를 사람이 이해 할 수 있도록 하는 과정을 문자 디코딩이라고 함
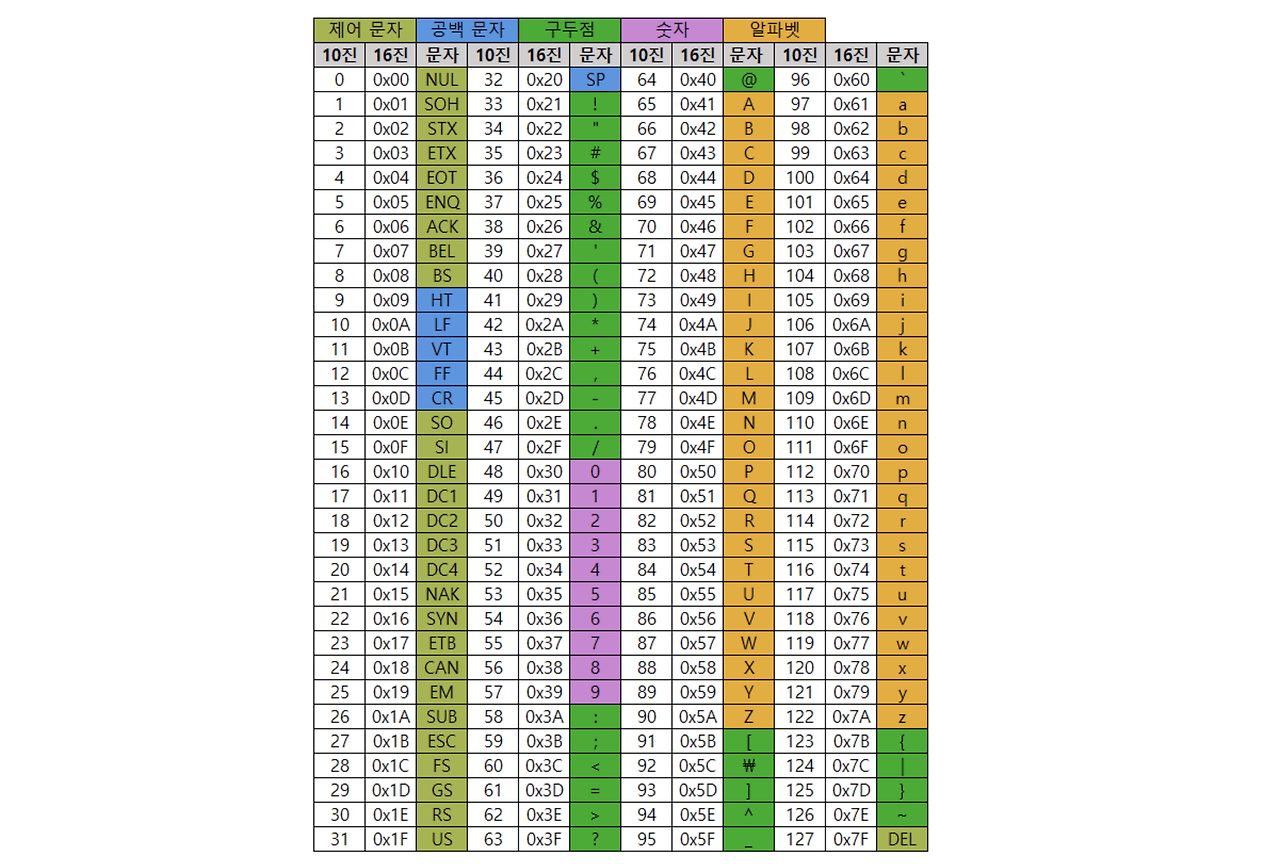
아스키 코드
- 초창기 문자 집합 중 하나로, 영어 알파벳과 아라비아 숫자 그리고 일부 특수 문자를 포함함
- 아스키 문자 집합에 속한 문자들은 각각 7비트로 표현되는데, 7비트로 표현할 수 있는 정보의 거짓수는 2의 7개로 총 128개의 문자를 표현 가능
- 실제로는 하나의 아스키 문자를 나타내기 위해 8비트(1바이트를 사용함)
- 하지만 8비트 중 1비트는 패리티 비트임
- 패리티 비트는 오류 검출을 위해 사용되는 비트이기에 실질적으로 문자 표현을 하기 위해 사용되는 비트는 7비트임
- 아스키 문자에 대응된 고유의 수를 아스키 코드라고 함
- 아스키 코드를 이진수로 표현함으로써 아스키 문자를 0과 1로 표현가능 o
- 문자 인코딩에서 글자에 부여된 고유의 값을 코드 포인트라고 함
- 예를 들어 A의 코드 포인트는 65임
- 확장 아스키란 다양한 문자 표현을 위해 아스키 코드에 1비트를 추가한것

EUC-KR
- 한글 인코딩에는 두 가지 방식, 완성형(한글 완성형 인코딩)과 조합형(한글 조합령 인코딩)이 존재함
- 완성형 인코딩은 초성 중성, 종성의 조합으로 이루어진 완성된 하나의 글자에 고유한 코드를 부여하는 인코딩 방식
- 예를 들어 가는 1, 나는 2, 다는 3
- 조합형 인코딩은 초성을 위한 비트열, 중성을 위한 비트열, 종성을 위하 비트열을 할당하여 그것들의 조합으로 하나의 글자를 완성해 가는 방식
- EUC-KR은 KS X1001, KS X 1003이라는 문자 집합을 기반으로 하는 대표적인 완성형 인코딩 방식
- 즉 EUC-KR 인코딩은 초성 중성, 종성이 모두 결합된 한글 단어에 2바이트 크기의 코드를 부여함
- EUC-KR로 인코딩된 한글은 네 자리 십육진수로 나타낼 수 있음
- CP949 버전은 EUC-KR 방식으로 표현할 수 없는 것을 해결하기 위해 마이크로소프트에서 만듦
유니코드와 UTF-8
- 유니코드는 EUC-KR보다 훨씬 다양한 한글을 포함하여 대부분 나라의 문자, 특수문자, 화살표나 이모티콘까지도 코드로 표현가능한 통일된 문자 집합임
- 현대 문자를 표현할 때 가장 많이 사용되는 표준 문자 집합이며, 인코딩 세계에서 매우 중요한 역할을 맡고 있음
- 유니코드 문자 집합에서는 아스키 코드나 EUC-KR과 같이 고유한 값이 부여됨
- 예를 들어 한에 부여된 값은 D55C(16), 글에 부여된 값은 AE00(16)임
- 유니코드 앞에 U+라는 문자열이 붙으면 이는 십육진수로 유니코드를 표현할때 사용하는 표기임
- 글자에 부여된 값 자체를 인코딩된 값으로 삼지 않고 다양한 방법으로 인코딩 하는 UTF-8, UTF-16, UTF-32가 있음
- 이는 유니코드 문자에 부여된 값을 인코딩 하는 방식
- UTF-8은 통상 1바이트부터 4바이트까지의 인코딩 결과를 만들어 냄

- 유니코드 문자에 부여된 값의 범위가 0부터 007F(16)까지는 1바이트로 표현
- 유니코드 문자에 부여된 값의 범위가 0080(16)부터 07FF(16)까지는 2바이트로 표현
- 유니코드 문자에 부여된 값의 범위가 0080(16)부터 FFFF(16)까지는 3바이트로 표현
- 유니코드 문자에 부여된 값의 범위가 10000(16부터 10FFFF(16)까지는 4바이트로 표현
그렇다면 한글은 몇 바이트로 구성될까?
한 = D55C(16)
글 = AE00(16)
두 글자 모두 0800(16)와 FFFF(16) 사이에 있기에 인코딩하면 3바이트로 표현되는 것을 예상할 수 있음

- 여기서 붉은색 x표가 있는 곳에 유니코드 문자에 부여한 고유의 값이 들어감
- 한 과 글에 부여된 값은 D55C(16), AE00(16)
- 이는 각각 이진수로 1101 0101 0101 1100(2), 1010 1110 0000 0000(2)임
- 한 과 글을 UTF-8의 방식으로 인코딩한 결과
11101101 10010101 10011100(2)
11101010 10111000 1000000(2)